Bases de mathématiques informatiques binaires, décimales, hexadécimaux, octaux
- 1761
- 537
- Jade Muller
La façon dont nous exprimons un nombre dépend du fait que nous soyons un ordinateur ou un humain. Si nous sommes humains, nous sommes susceptibles d'exprimer des nombres en utilisant notre familier Bas-base système décimal. Si nous sommes un ordinateur, nous sommes probablement, à notre cœur, d'exprimer des nombres comme 2 bases ou binaire.
Alors qu'est-ce qui se passe avec toutes les nombreuses façons d'exprimer des nombres, et pourquoi existent-ils? Cet article entrera dans des détails et, espérons-le, à la fin, vous comptez octal sur vos doigts. Ce qui fonctionne bien au fait, tant que vous n'utilisez que 8 doigts, après tout… Octal est 8 bases.
Dans ce tutoriel, vous apprendrez:
- Comment faire un comptage simple dans des systèmes non décimaux UP comme le binaire, l'hexadécimal et l'octale.
- Quelles termes 2 bases, 10 bases etc. Demandez et comment les comprendre plus facilement.
- La connexion entre ces différentes méthodes d'exprimer des nombres
Bases de mathématiques informatiques: binaire, décimal, hexadécimal, octal Exigences et conventions logicielles utilisées
| Catégorie | Exigences, conventions ou version logicielle utilisée |
|---|---|
| Système | Indépendant de la distribution Linux |
| Logiciel | Ligne de commande bash, système basé sur Linux |
| Autre | Toute utilité qui n'est pas incluse dans le shell bash par défaut peut être installée en utilisant Sudo Apt-Get Install Utility-Name (ou Installation de miam pour les systèmes basés sur Redhat) |
| Conventions | # - nécessite que les commandes Linux soient exécutées avec des privilèges racine soit directement en tant qu'utilisateur racine, soit par l'utilisation de Sudo commande$ - exige que les commandes Linux soient exécutées en tant qu'utilisateur régulier non privilégié |
Décimal
Nous sommes tous très familiers avec le système décimal: 1 à 10 ou mieux 0 à 9, Le système même que nous avons pensé dès le premier jour de l'école et même avant par nos parents. Mais ce système numérique n'est pas tout ce qu'il y a. C'est juste l'un d'eux. Nous appelons ce système particulier Bas-base car il a une base de 10 caractères à savoir 0 à 9.
En décimal, nous pouvons compter facilement en utilisant simplement ce que nous avons pensé: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Nous n'avons pas besoin d'exercer des efforts pour cela, et cela vient naturellement. Cependant, si vous y réfléchissez vraiment, il n'y a pas de connexion logique réelle entre le numéro de mot «zéro» et «un» et «un» et «deux» et ainsi de suite. En dehors, avec le temps, nous comprenons que 0 + 1 = 1 et 1 + 1 = 2, mais il n'y a pas de réel et de substantiel direct autre connexion entre un et deux, 1 et 2. C'est juste une forme d'expression.
Pour en illustrer, considérez les affirmations ci-dessus par rapport à un fictif À 5 bases système. Il est beaucoup plus difficile pour nos esprits, car ils n'ont pas été formés à la même chose, à compter dans un système à 5 bases. Rendons-le encore plus difficile et indiquons que nos 5 nombres sont exprimés comme (, ), +, = et . respectivement. Comptons à 11 devons-nous?
0: (1:) 2: + 3: = 4: . 5:) (6:)) 7 :) + 8 :) = 9 :). 10: + (11: +)
À gauche, nous avons des nombres décimaux à 10 bases, à droite, nous avons notre système numérique auto-généré à 5 bases comptant de la même manière (et la gauche et la droite ont des valeurs numériques égales, i.e. dix en décimal / 10-base est +( Dans notre système numérique à 5 bases!).
Je peux compter très facilement de cette façon car je suis très habitué à comment base X Systèmes fonctionnent. Si vous regardez un peu plus près du décompte, vous découvrirez rapidement comment cela fonctionne et verrez comment il se compare à notre système de comptage basé sur les décimales. L'indice est le suivant; Une fois que vous manquez de personnages, vous préfixez simplement le premier personnage avec le premier personnage, en faisant deux personnages. Pourtant, comment écririez-vous 100? Devez-vous travailler tout le long de la liste? Probablement comme nos esprits ne sont pas utilisés pour énumer les choses en utilisant ces symboles.
Nos esprits comprennent décimal et luttent avec la plupart des autres base X Systèmes numériques basés sur lesquels x n'est pas 10. Peut-être un exemple? Veuillez calculer )) (((A == - () b… (+ où nous avons utilisé UN pour indiquer la multiplication, et B est simple plus. Mais il n'y a rien de similaire à ce sujet,? Pourtant, si nous avons converti ceci en décimales et notre familier + et X symboles, nous ne trouverions probablement pas ces équations.
Maintenant que nous sommes armés d'une compréhension de ce base X l'est vraiment, le reste est beaucoup plus facile. Et je le promets: plus d'étranges symboles pour exprimer des nombres, eh bien c'est jusqu'à ce que nous arrivions à l'hexadécimal 😉
Binaire
Jusqu'à ce que les ordinateurs quantiques frappent nos magasins informatiques locaux, nos ordinateurs sont assez limités. La seule chose, à son cœur, ce qu'un ordinateur comprend est pouvoir ou aucune puissance. Rien d'autre! Un ordinateur comprend simplement la puissance ou pas de puissance, mais elle ne "comprendre" Quel personnage un est, ou quel chiffre 9 est. Toutes ces choses, et bien plus encore (je.e. Tout le code informatique) à son noyau est exprimé autant de puissance ou pas de puissance.
Une seule telle unité de stockage et d'expression est appelée un bit. Un peu est l'unité de stockage le plus bas, le plus de niveau d'un ordinateur. UN bit ne peut stocker qu'un seul 0 ou un seul 1. En fait, il ne peut même pas stocker un zéro ou un 1), ou pas de pouvoir (notre 0). Vous pouvez commencer à voir comment fonctionne à 2 bases, ou binaire: il n'a que deux expressions: 0 et 1, Pas de puissance ni de puissance.
Si vous imaginez ceci en termes de matériel informatique physique, vous pouvez imaginer un lecteur de disque dur de type plus ancien en tant que plaque pleine de nombreux petits endroits qui ont soit de la puissance (magnétisé) ou n'ont pas de puissance (ne sont pas magnétisés). Si vous l'imaginez sous forme de données sur un câble, vous pouvez l'imaginer en puissance ou pas d'alimentation.
Alors faisons notre même comptage à 11 mais cette fois en utilisant nos deux seules méthodes d'expression possibles, les nombres de notre système numérique binaire: 0 et 1.
0: 0 1: 1 2: 10 3: 11 4: 100 5: 101 6: 110 7: 111 8: 1000 9: 1001 10: 1010 11: 1011
À gauche, nous avons une décimale à 10 bases, et à droite, nous avons un binaire à 2 bases.
Une fois que vous voir, Il est facile de compter: commencez simplement par 0 et 1, et notez comment 0 a toujours une signification particulière: quand vous venez à 2 en décimal, ce n'est pas 01 (je.e. le premier personnage utilisé comme nouveau personnage le plus à gauche), mais plutôt dix Comme 0 a la valeur réelle de zéro. En d'autres termes, vous n'écririez pas: 0, 1, 2, 3,…, 8, 9, 00 ou 01, car aucun n'a de sens; on écrire 10. La même chose s'applique ici.
Il en va de même dans notre système à 5 bases ci-dessus: nous avons utilisé ) ( Pour exprimer l'étape suivante après que tous nos chiffres ont été utilisés, et non (( ce qui serait incorrect. Ce serait comme écrire 00 au lieu de 6.
Une fois que vous connaissez ces étapes de base qui s'appliquent à tous les systèmes X-base, il devient plus facile de compter. Et vous pouvez utiliser Continuez à ajouter un personnage le plus à gauche le plus à gauche et réinitialiser le caractère le plus à droite actuellement utilisé, chaque fois que vous manquez de prochaines étapes numériques possibles en utilisant uniquement la longueur que vous avez pour le moment. Lisez quelques fois des étapes binaires et regardez la progression, et bientôt vous pourrez compter sur le binaire, même sans utiliser de doigts. Si vous utilisez des doigts, n'oubliez pas d'utiliser seulement deux.
Hexadécimal
Alors maintenant que nous avons exploré 10-base, 2 bases (et 5-base 😉 Regardons quelque chose qui peut sembler étrange à nouveau à première vue: 16-base. Comment pourrions-nous intégrer 16 combinaisons numériques possibles en un seul caractère? Bienvenue sur hexadécimal, qui utilise des lettres.
Faisons un simple nombre d'abord: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
16 caractères au total, le système hexadécimal utilise A-F une fois qu'il manque de moyens d'exprimer le numéro suivant dans la serie. Compter de un à 11 comme nous l'avons fait auparavant ici, car il y a tout simplement exprimé par «B». Alors commençons un peu plus loin dans le processus cette fois:
0: 0 1: 1… 9: 9 10: A… 15: F 16: 10 17: 11
À gauche, nous avons une décimale à 10 bases, et à droite, nous avons 16 bases hexadécimal. Il est donc plus facile de se rappeler, notez que Hexa-Decimal nous fait réfléchir à 6-10.
Aie! Maintenant nous nous retrouvons avec dix en 16 bases hexadécimal qui vaut vraiment 16 en décimal à 10 bases! Cela peut être légèrement déroutant et on peut immédiatement voir la nécessité de comprendre clairement avec quel système numérique nous travaillons pour éviter les erreurs coûteuses.
De nombreux calculatrices de divers systèmes d'exploitation ont un paramètre de développeur ou d'ordinateur qui peut être activé pour fonctionner avec différents systèmes numériques. Certains vont un peu plus loin et vous montrent très clairement ce que le nombre à portée de main se traduirait dans divers autres systèmes numériques X-Base, comme cette grande calculatrice incluse dans Linux Mint 20:
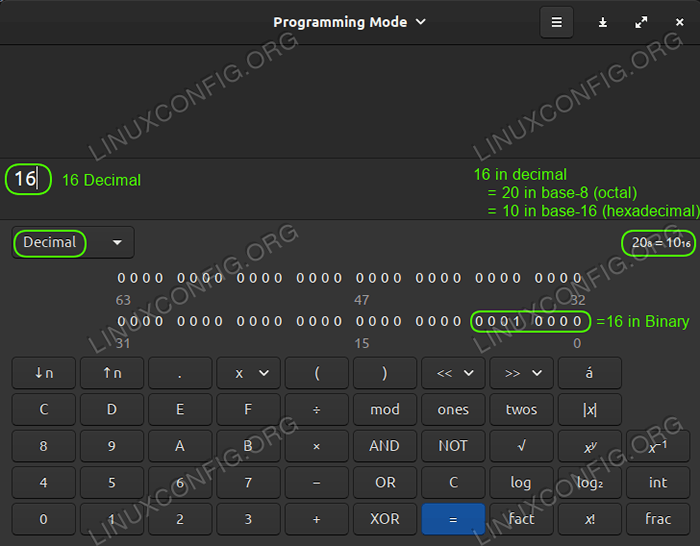Calculatrice de Linux Mint 20 montrant décimal, binaire, hexadécimal, octal tout à la fois Octal
Maintenant que nous avons vu les systèmes numériques précédents, il est plus facile de voir comment nous pouvons compter dans un système à 8 bases, en l'occurrence octal, Un autre système utilisé en conjonction avec et par des systèmes de traitement informatique.
En octal, nous avons 8 caractères numériques étant 0, 1, 2,…, 6, 7. Comptons à 11 dans un système numérique à 8 bases, à partir de 7:
7: 7 8: 10 9: 11 10: 12 11: 13
À gauche, nous avons une décimale à 10 bases, et à droite, nous avons un octal à 8 bases.
Encore une fois, nous pouvons voir un peu déroutant dix en 10 bases décimales 12 en 8 bases octal.
Pourquoi tant de systèmes numériques?
Alors pourquoi y a-t-il tant de systèmes numériques différents? La raison est simple. Rappelez-vous comment un bit était un magasin pour placer un zéro binaire ou un? Eh bien, si vous prenez 8 bits, vous aurez un octet et un octet est souvent utilisé pour exprimer des caractères alpha-nucléaires simples. Si vous pensez à la façon dont 8 est vraiment à la base de cela, il ne devrait pas être trop loin pour voir octal (8) s'adapter aux systèmes numériques utilisés sur les ordinateurs.
Ensuite, nous avons hexadécimal, qui est vraiment de 2 x 8 = 16 caractères. Et ici, nous avons 16 bits (ou 2 octets) représentés comme un seul caractère. Tout se bloque étroitement et entre vraiment en jeu lorsque vous considérez comment les caractères alpha-nucléaires sont utilisés et traités dans des systèmes informatiques. Par exemple, certains caractères spéciaux (comme par exemple des caractères japonais ou chinois) peuvent nécessiter deux ou trois octets pour les stocker (multi-octets).
Divers systèmes numériques simplifient les nombreux types de flux de données qui se produisent dans un ordinateur, et en fonction des flux à portée de main, et tous les algorithmes informatiques correspondants sélectionnés ou utilisés, diverses optimisations sont possible. La plupart des langues en développement ont, par exemple, un traitement binaire et potentiellement hexadécimal hautement optimisé en plus du traitement décimal.
Conclusion
Dans cet article, nous avons plongé dans des systèmes numériques à 2 bases, 10 bases, 16 bases et 8 bases, étant binaires (2), décimaux (10), hexadécimaux (16) et octal (8). Nous avons vu quel type de connexions il y a entre ceux-ci, et comment faire un comptage simple dans tous ces systèmes.
Apprendre un peu plus sur le fonctionnement des ordinateurs aide souvent, surtout quand il s'agit de faire des premiers programmes informatiques ou de comprendre la théorie. Quand on devient un développeur à temps plein, à ce stade, tous ces systèmes sont une seconde nature, et ils sont souvent utilisés dans le code réel.
Veuillez nous laisser un commentaire avec vos idées sur ces systèmes numériques! Et si vous êtes prêt à apprendre des choses plus intéressantes, jetez un œil à notre manipulation de Big Data pour le plaisir et le profit de l'article 1! Apprécier!
Tutoriels Linux connexes:
- Tutoriel de débogage GDB pour les débutants
- Une introduction à l'automatisation Linux, des outils et des techniques
- Choses à installer sur Ubuntu 20.04
- Mint 20: Mieux que Ubuntu et Microsoft Windows?
- Système linux hung? Comment s'échapper vers la ligne de commande et…
- Choses à faire après l'installation d'Ubuntu 20.04 Focal Fossa Linux
- Comment faire des calculs décimaux en bash en utilisant la Colombie-Britannique
- Masterring Bash Script Loops
- Ubuntu 20.04 Guide
- Choses à faire après l'installation d'Ubuntu 22.04 Jammy Jellyfish…