Suggérer un moyen plus simple d'ajouter des fractions
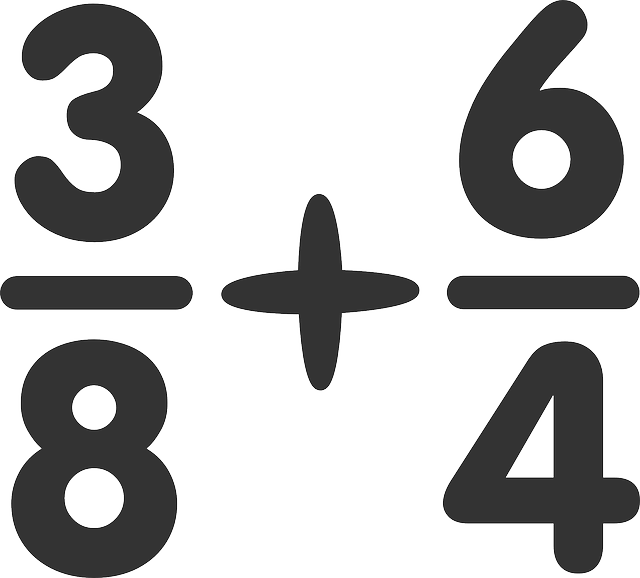
- 2799
- 351
- Noa Faure
Eh bien, les fractions peuvent être vraiment effrayantes, je dois admettre. Ajouter des fractions est encore plus effrayant. Il semble qu'ils soient le point de départ de la peur du monde des mathématiques. Jusqu'à ce que vous réalisiez que gérer les fractions est également aussi simple que de gérer les nombres naturels, si vous connaissez l'astuce.
Méthodes pour ajouter des fractions
Méthode 1
1. Comprenons d'abord la terminologie des fractions avant de passer à des étapes pour ajouter des fractions. Une fraction a deux parties - numérateur et dénominateur. Si vous voulez vraiment devenir un érudit en fractions, vous pouvez visiter la page de fraction sur Wikipedia.
Le numérateur est le nombre au-dessus de la ligne dans une fraction et le dénominateur est le nombre sous la ligne.
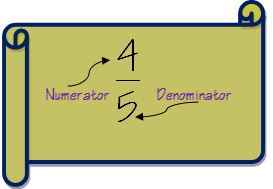
La première étape pour ajouter des fractions consiste à vérifier les dénominateurs des deux fractions. C'est le dénominateur des deux fractions est le même alors que l'ajout devient très simple.
Dans un tel cas, nous devons simplement ajouter les numérateurs et le dénominateur restera le même.
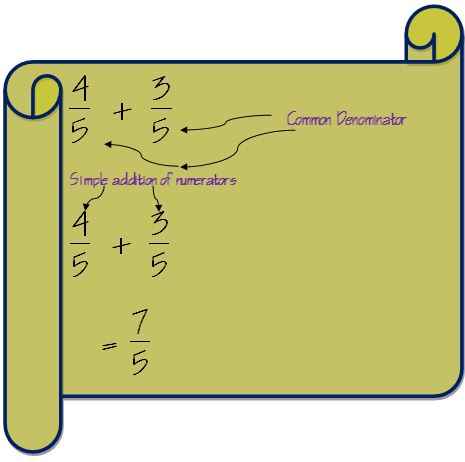
Mais si les dénominateurs ne sont pas les mêmes, nous devons faire les dénominateurs des deux fractions. La méthode à faire est de trouver le multiple le moins courant des dénominateurs.
Comment trouver le moins commun multiple
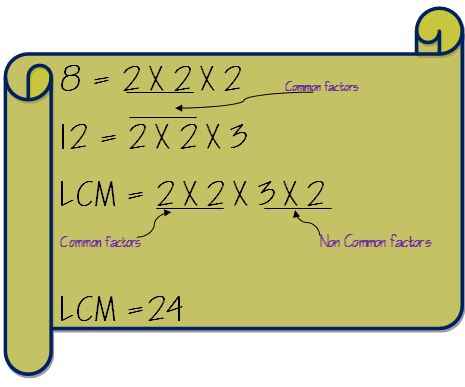
Disons que nous devons trouver LCM de deux numéros 8 et 12.
Écrivez d'abord les facteurs premiers des deux nombres séparément.
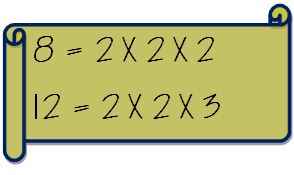
Maintenant, retirez les facteurs communs et multipliez-le avec les facteurs non communs. Ainsi, le LCM de 8 et 12 sera calculé comme suivant.
Ajouter des fractions avec différents dénominateurs
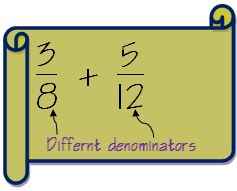
Disons que nous avons deux fractions 3/8 et 5/12
Les étapes sont:
1. Vérifiez si les dénominateurs sont les mêmes pour les deux fractions. Si les dénominateurs sont les mêmes, nous suivons la méthode mentionnée ci-dessus. Dans notre cas, ils sont différents.
2. Découvrez le LCM du dénominateur. Comme illustré au-dessus du LCM pour 8 et 12 est 24.
3. Faire les deux dénominateurs identiques que le LCM en multipliant avec des nombres appropriés.

4. Si nous avons multiplié le dénominateur par un nombre, nous devons également multiplier le numérateur par le même nombre également pour garder la fraction intacte.

5. En effectuant ces étapes, nous obtenons deux fractions dont les dénominateurs sont les mêmes. Nous devons donc simplement ajouter les numérateurs comme nous l'avons fait dans notre exemple précédent.

6. Nous obtenons le résultat comme 19/24
7. Nous devons vérifier s'il y a un facteur commun entre le numérateur et le dénominateur ou non après l'addition.
8. S'il n'y a pas de facteur commun, nous pouvons signaler le résultat comme notre réponse finale.

Méthode 2
Cette méthode nous donnera également le résultat souhaité, mais il n'est pas suggéré pour les élèves de cinquième année qui veulent apprendre à ajouter des fractions.
1. Convertir à la fois la fraction en nombres en divisant le numérateur par dénominateur
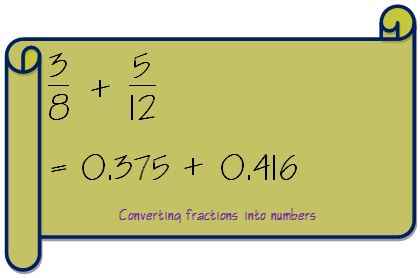
2. Maintenant, c'est un simple ajout de deux nombres
3. Ajoutez les deux nombres pour obtenir la réponse

Veuillez noter que les réponses que nous avons obtenues dans la méthode 1 et la méthode 2 pour ajouter des fractions sont les mêmes. La réponse par la méthode 1 est 19/24. Si nous divisons 19 par 24, nous obtiendrons la réponse comme 0.791, c'est ce que nous avons obtenu par la méthode 2.
- « Ajouter une image - Créez une page Web géniale
- Ajouter une signature Outlook - Envoyer un e-mail comme un boss »

