Introduction
- 1945
- 262
- Mohamed Brunet
Dans ce tutoriel rapide GNU r aux modèles et graphiques statistiques, nous fournirons un exemple de régression linéaire simple et apprendre à effectuer une telle analyse statistique de base des données. Cette analyse sera accompagnée d'exemples graphiques, ce qui nous rapprochera de la production de parcelles et de graphiques avec GNU R. Si vous n'êtes pas du tout familier avec l'utilisation de R, veuillez consulter le tutoriel préalable: un tutoriel rapide aux opérations, fonctions et structures de données de base.
Modèles et formules en r
Nous comprenons un modèle dans les statistiques comme une description concise des données. Une telle présentation de données est généralement présentée avec un formule mathématique. R a sa propre façon de représenter les relations entre les variables. Par exemple, la relation suivante y = c0+c1X1+c2X2+… + CnXn+r est en r écrit comme
y ~ x1 + x2 +… + xn,
qui est un objet de formule.
Exemple de régression linéaire
Fournissons maintenant un exemple de régression linéaire pour GNU R, qui se compose de deux parties. Dans la première partie de cet exemple, nous étudierons une relation entre les rendements de l'indice financier libellé dans le dollar américain et de tels rendements libellés en dollars canadiens. De plus, dans la deuxième partie de l'exemple, nous ajoutons une variable supplémentaire à notre analyse, qui sont des rendements de l'indice libellé en euro.
Régression linéaire simple
Téléchargez l'exemple de fichier de données dans votre répertoire de travail: régression-example-GNU-R.CSV
Laissez maintenant exécuter R dans Linux à partir de l'emplacement du répertoire de travail simplement par
$ R
et lire les données de notre exemple de fichier de données:
> retourne<-read.csv("regression-example-gnu-r.csv",header=TRUE) Vous pouvez voir les noms des variables tapant
> Noms (retourne)
[1] "USA" "Canada" "Allemagne"
Il est temps de définir notre modèle statistique et d'exécuter une régression linéaire. Cela peut être fait dans les quelques lignes de code suivantes:
> y<-returns[,1]
> x1<-returns[,2]
> retourne.LM<-lm(formula=y~x1)
Pour afficher le résumé de l'analyse de régression, nous exécutons le résumé() Fonction sur l'objet retourné Retour.LM. C'est,
> Résumé (retourne.LM)
Appel:
lm (formule = y ~ x1)
Résidus:
Min 1Q médian 3Q max
-0.038044 -0.001622 0.000001 0.001631 0.050251
Coefficients:
Estimer les MST. Erreur t Valeur Pr (> | T |)
(Intercepter) 3.174E-05 3.862E-05 0.822 0.411
x1 9.275E-01 4.880E-03 190.062 <2e-16 ***
---
Signifier. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Erreur standard résiduelle: 0.003921 à 10332 degrés de liberté
Multiples R-carré: 0.7776, R-Squared ajusté: 0.7776
F-statistique: 3.612E + 04 sur 1 et 10332 df, valeur p: < 2.2e-16
Cette fonction sortira le résultat correspondant ci-dessus. Les coefficients estimés sont ici C0~ 3.174E-05 et C1 ~ 9.275E-01. Les valeurs de p ci-dessus suggèrent que l'interception estimée C0 n'est pas significativement différent de zéro, donc il peut être négligé. Le deuxième coefficient est significativement différent de zéro depuis la valeur p<2e-16. Therefore, our estimated model is represented by: y=0.93 x1. De plus, R-Squared est 0.78, ce qui signifie qu'environ 78% de la variance de la variable y s'explique par le modèle.
La régression linéaire multiple
Laissez maintenant ajouter une variable supplémentaire dans notre modèle et effectuer une analyse de régression multiple. La question est maintenant de savoir si l'ajout d'une variable supplémentaire à notre modèle produit un modèle plus fiable.
> x2<-returns[,3]
> retourne.LM<-lm(formula=y~x1+x2)
> Résumé (retourne.LM)
Appel:
lm (formule = y ~ x1 + x2)
Résidus:
Min 1Q médian 3Q max
-0.0244426 -0.0016599 0.0000053 0.0016889 0.0259443
Coefficients:
Estimer les MST. Erreur t Valeur Pr (> | T |)
(Intercepter) 2.385E-05 3.035E-05 0.786 0.432
x1 6.736E-01 4.978E-03 135.307 <2e-16 ***
x2 3.026E-01 3.783E-03 80.001 <2e-16 ***
---
Signifier. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Erreur standard résiduelle: 0.003081 sur 10331 degrés de liberté
Multiples R-carré: 0.8627, R-Squared ajusté: 0.8626
F-statistique: 3.245e + 04 sur 2 et 10331 df, valeur p: < 2.2e-16
Ci-dessus, nous pouvons voir le résultat de l'analyse de régression multiple après avoir ajouté la variable x2. Cette variable représente les rendements de l'indice financier en euro. Nous obtenons maintenant un modèle plus fiable, car le R-Squared ajusté est 0.86, qui est plus élevé alors la valeur obtenue avant égale à 0.76. Notez que nous avons comparé le R-Squared ajusté car il prend en compte le nombre de valeurs et la taille de l'échantillon. Encore une fois, le coefficient d'interception n'est pas significatif, par conséquent, le modèle estimé peut être représenté comme: y = 0.67x1+0.30x2.
Notez également que nous aurions pu faire référence à nos vecteurs de données par leurs noms, par exemple
> LM (renvoie $ USA ~ Renvoie $ Canada)
Appel:
LM (Formule = Renvoie $ USA ~ Renvoie $ Canada)
Coefficients:
(Interception) Renvoie $ Canada
3.174E-05 9.275E-01
Graphique
Dans cette section, nous montrerons comment utiliser R pour la visualisation de certaines propriétés dans les données. Nous illustrons des chiffres obtenus par des fonctions telles que parcelle(), boxplot (), hist (), qqnorm ().
Plot de dispersion
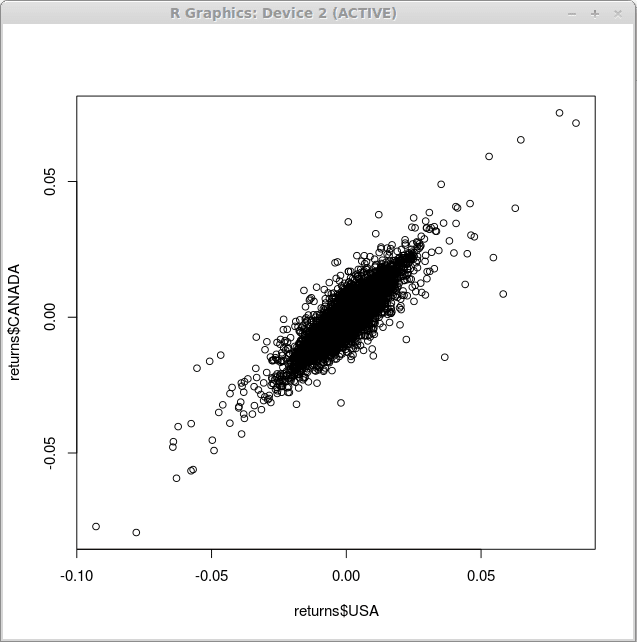
Probablement le plus simple de tous les graphiques que vous pouvez obtenir avec r est le tracé de dispersion. Pour illustrer la relation entre la dénomination du dollar américain des rendements de l'indice financier et la dénomination du dollar canadien, nous utilisons la fonction parcelle() comme suit:
> Terrain (renvoie $ USA, retourne $ canada)
À la suite de l'exécution de cette fonction, nous obtenons un diagramme de dispersion comme indiqué ci-dessous

L'un des arguments les plus importants que vous pouvez transmettre à la fonction parcelle() est «type». Il détermine quel type de tracé doit être dessiné. Les types possibles sont:
• '"p«'Pour * p * oints
• '"l«'Pour * l * Ines
• '"b"' pour les deux
• '"c"'Pour la partie des lignes seule de'" B "'
• '"o«'Pour les deux' * o * verplotted '
• '"H«'Pour' * h * istogram 'comme (ou' haute densité ') lignes verticales
• '"s«'Pour les teps d'escalier *
• '"S«'Pour un autre type de * s * teps
• '"n«'Pour aucun complot
Pour superposer une ligne de régression sur le diagramme de dispersion ci-dessus, nous utilisons le courbe() fonction avec l'argument «ajouter» et «col», qui détermine que la ligne doit être ajoutée au tracé existant et à la couleur de la ligne tracée, respectivement.
> courbe (0.93 * x, -0.1,0.1, add = true, col = 2)
Par conséquent, nous obtenons les modifications suivantes dans notre graphique:
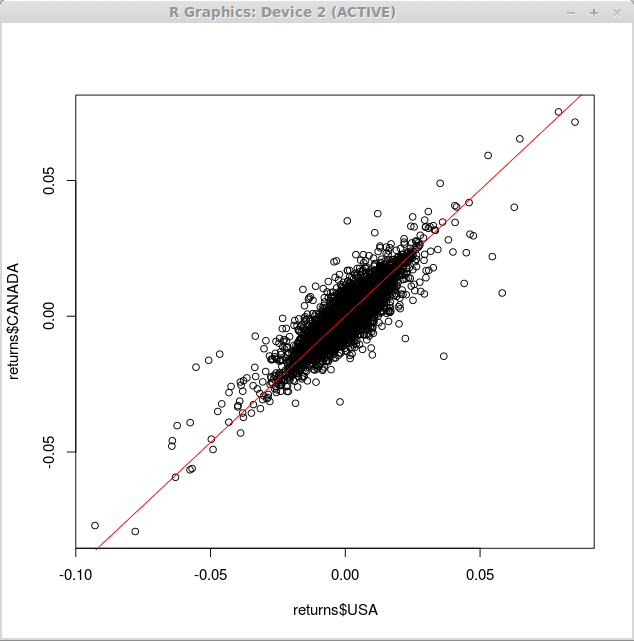
Pour plus d'informations sur le tracé de fonction () ou les lignes () Utilisez la fonction aider(), par exemple
> Aide (tracé)
Tracé de la boîte
Voyons maintenant comment utiliser le boxplot () fonction pour illustrer les statistiques descriptives de données. Premièrement, produire un résumé des statistiques descriptives pour nos données par le résumé() fonction puis exécuter le boxplot () Fonction pour nos retours:
> Résumé (retour)
USA Canada Allemagne
Min. : -0.0928805 min. : -0.0792810 min. : -0.0901134
1er qu.: -0.0036463 1er qu.: -0.0038282 1st Qu.: -0.0046976
Médian: 0.0005977 médiane: 0.0005318 médiane: 0.0005021
Moyenne: 0.0003897 Moyenne: 0.0003859 Moyenne: 0.0003499
3e qu.: 0.0046566 3rd Qu.: 0.0047591 3rd Qu.: 0.0056872
Max. : 0.0852364 Max. : 0.0752731 Max. : 0.0927688
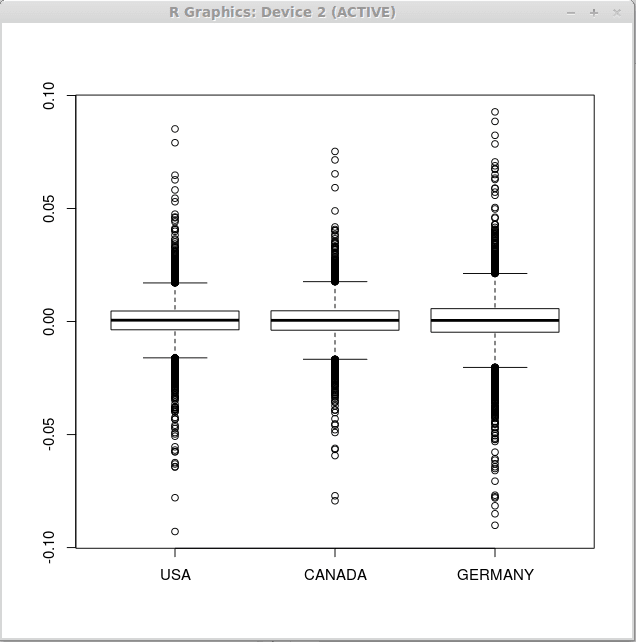
Notez que les statistiques descriptives sont similaires pour les trois vecteurs, nous pouvons donc nous attendre à des boîtes à boîte similaire pour tous les ensembles de rendements financiers. Maintenant, exécutez la fonction boxplot () comme suit
> boxplot (retourne)
En conséquence, nous obtenons les trois boîtes à boîte suivantes suivantes.
Histogramme
Dans cette section, nous examinerons les histogrammes. L'histogramme de fréquence a déjà été introduit dans l'introduction de GNU R sur le système d'exploitation Linux. Nous allons maintenant produire l'histogramme de densité pour les rendements normalisés et le comparer avec la courbe de densité normale.
Normalisons d'abord les rendements de l'indice libellé en dollars américains pour obtenir zéro moyenne et variance égale à un afin de pouvoir comparer les données réelles avec la fonction de densité normale standard théorique standard.
> RETUS.norme<-(returns$USA-mean(returns$USA))/sqrt(var(returns$USA))
> Moyenne (retus.norme)
[1] -1.053152E-17
> var (retus.norme)
[1] 1
Maintenant, nous produisons l'histogramme de densité pour de tels rendements normalisés et tracez une courbe de densité normale standard sur un tel histogramme. Cela peut être réalisé par l'expression r suivante
> Hist (retus.Norm, Breaks = 50, Freq = False)
> courbe (dnorm (x), - 10,10, add = true, col = 2)
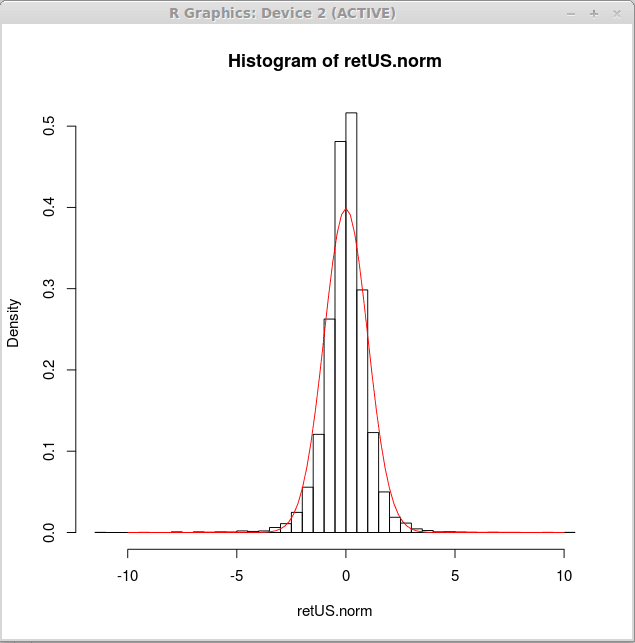
Visuellement, la courbe normale ne correspond pas bien aux données. Une distribution différente peut être plus adaptée aux rendements financiers. Nous apprendrons à adapter une distribution aux données dans des articles ultérieurs. Pour le moment, nous pouvons conclure que la distribution la plus appropriée sera plus choisie au milieu et aura des queues plus lourdes.
QQ-PLOT
Un autre graphique utile dans l'analyse statistique est le QQ-Plot. Le Plot QQ est un tracé quantile quantile quantile, qui compare les quantiles de la densité empirique aux quantiles de la densité théorique. Si ceux-ci correspondent bien, nous devrions voir une ligne droite. Comparons maintenant la distribution des résidus obtenus par notre analyse de régression ci-dessus. Tout d'abord, nous obtiendrons un PLOT QQ pour la régression linéaire simple puis pour la régression linéaire multiple. Le type de la place QQ que nous utiliserons est le Plot QQ normal, ce qui signifie que les quantiles théoriques du graphique correspondent aux quantiles de la distribution normale.
Le premier tracé correspondant aux simples résidus de régression linéaire est obtenu par la fonction qqnorm () de la manière suivante:
> retourne.LM<-lm(returns$US~returns$CANADA)
> qqnorm (retourne.LM $ résidus)
Le graphique correspondant s'affiche ci-dessous:
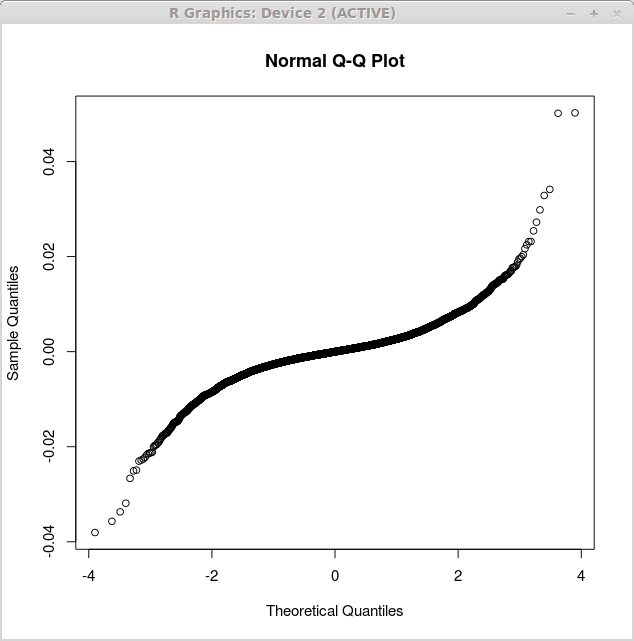
Le deuxième tracé correspond aux multiples résidus de régression linéaire et est obtenu comme:
> retourne.LM<-lm(returns$US~returns$CANADA+returns$GERMANY)
> qqnorm (retourne.LM $ résidus)
Ce tracé est affiché ci-dessous:
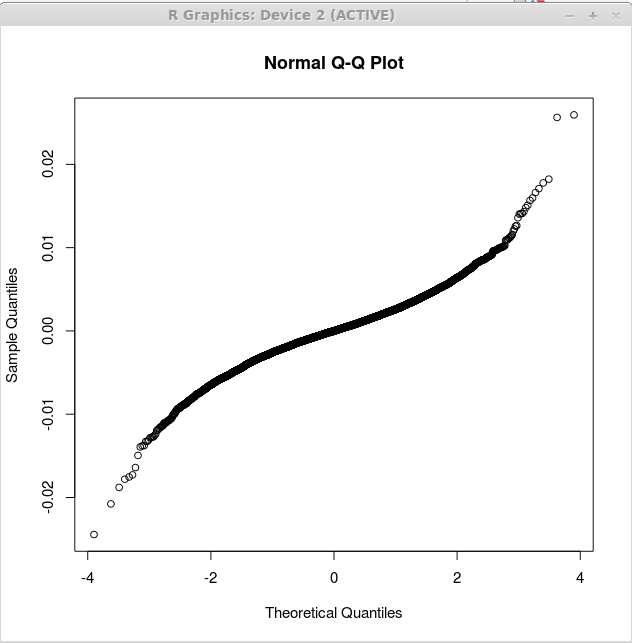
Notez que le deuxième tracé est plus proche de la ligne droite. Cela suggère que les résidus produits par l'analyse de régression multiple sont plus proches de la distribution normalement. Cela prend en charge le deuxième modèle comme plus utile sur le premier modèle de régression.
Conclusion
Dans cet article, nous avons introduit la modélisation statistique avec GNU R sur l'exemple de la régression linéaire. Nous avons également discuté de certains graphiques de statistiques fréquemment utilisés. J'espère que cela a ouvert une porte à une analyse statistique avec GNU R pour vous. Nous discuterons, dans les articles ultérieurs, discuterons des applications plus complexes de R pour la modélisation statistique ainsi que la programmation, alors continuez à lire.
Série de tutoriels GNU R:
Partie I: Tutoriels d'introduction à GNU R:
- Introduction à GNU R sur le système d'exploitation Linux
- Exécution de GNU R sur le système d'exploitation Linux
- Un tutoriel rapide sur les opérations de base, les fonctions et les structures de données
- Un tutoriel rapide sur les modèles et graphiques statistiques
- Comment installer et utiliser des packages dans GNU R
- Construire des packages de base à GNU R
Partie II: Langue Gnu r:
- Un aperçu du langage de programmation GNU R
Tutoriels Linux connexes:
- Une introduction à l'automatisation Linux, des outils et des techniques
- Choses à installer sur Ubuntu 20.04
- Masterring Bash Script Loops
- Choses à faire après l'installation d'Ubuntu 20.04 Focal Fossa Linux
- Boucles imbriquées dans les scripts bash
- Mint 20: Mieux que Ubuntu et Microsoft Windows?
- Gestion de la saisie des utilisateurs dans les scripts bash
- Ubuntu 20.04 astuces et choses que vous ne savez peut-être pas
- Manipulation de Big Data pour le plaisir et le profit Partie 1
- Ubuntu 20.04 Guide

